How ECL changes the value of interventions that broadly benefit distant civilizations
Previously, I gave a broad overview of potentially decision-relevant implications of ECL.
Here, I want to zoom in on ECL’s relevance for the following type of intervention: Making misaligned AI behave in a better way towards distant civilizations. (Either alien civilizations that it encounters within the causally affectable universe, or civilizations that it never encounters physically, but can infer the existence of.1)
Some candidate interventions in this class are:
Roughly shaping AI values to avoid giving the AI values that would make interactions with others go worse (e.g. spitefulness or value-based unwillingness to compromise) or to increase the likelihood that such interactions go especially well (e.g. Bostrom’s idea of value porosity.)
Preventing AI from making early bad decisions. (Motivated by e.g. commitment races. The focus on early decisions is because it’s easier for us to affect decisions that are made closer in time to our interventions.)
Here’s one way in which ECL is relevant for this: An additional candidate intervention to put on the list is “make misaligned AI sympathetic to ECL”.
But I won’t say any more about that in this post. Instead, my focus is:
How much does ECL raise the importance of this whole class of interventions, via making us care more about distant civilizations?
Note that I won’t talk about the “baseline importance” of such interventions, before taking ECL into account.
I’ll talk about:
How much more do we care about this if we do ECL with distant evolved aliens? (Compared to if we don’t do ECL at all.)
Tentative answer: A bit more. Maybe something like 1.5-10x more.
How much more do we care about this if we do ECL with distant misaligned AIs? (Compared to if we only do ECL with distant evolved aliens.)
Tentative answer: Not much more.
What about distant actors that don’t go into either of those categories?
Tentative answer: Seems hard to tell!
This post will be fairly math-heavy. Feel free to skip it if you’re not up for that.
The setting I’m looking at
I will be looking at a very abstract problem that captures some of the key dynamics. In particular, in order to study:
How much does ECL raise the importance of this whole class of interventions, via making us care more about distant civilizations?
I will be looking at:
How much does ECL raise the importance of interventions that broadly benefit a variety of beneficiaries with different values, compared to interventions that mainly benefit our own values?
Using the following model:
There’s some large number of distant civilizations.
I will be talking about N civilizations indexed between 1 and N.2
Each of those civilizations has some particular values. When I talk about a civilization being benefitted or harmed, I’m actually talking about their values being benefitted or harmed.
In particular, I want to assume that the degree to which we care about effects on distant civilizations is proportional to how much their values overlap with our values. (How much “the things they care about” overlap with “the things we care about”.)
As a stand-in for interventions that “benefit a variety of beneficiaries with different values”, I’ll talk about interventions that benefit a random, distant civilization.
This captures how such interventions look more promising if a large fraction of the potentially-benefitted civilizations have similar values to us. And how the interventions look less promising if we’re indifferent to benefits and harms to most civilizations’ values.
It also puts to the side questions like “how many civilizations like these are there?” and “exactly how do these benefits/harms work?” which I prefer to tackle separately. (Not in this post.)
I will operate in an expected-utility framework, where we e.g. care twice as much about things that happen with twice the probability, and where we can talk about benefitting someone by x units (which we would care about x times as much as 1 unit).
Here is some notation. I will denote the overlap between our (universe-wide) values and the values of civilization i as v(i). The number v(i) will have the following properties:
If v(i) is equal to 1, that means that we care equally much about benefits to our own universe-wide values and civilization i’s universe-wide values.
The degree to which we care about benefiting the values of civilization i is proportional to v(i). This means, for example, that:
If v(i) is half as large as v(j), then we are indifferent between benefitting v(i) for sure and benefitting v(j) with 50% probability.
If v(i) is equally large as v(j) + v(k), then we are indifferent between benefitting v(i) or benefitting both v(j) and v(k).
For simplicity, I will assume that all the actors inside a civilization share that civilization’s values — meaning that v(i) is at most 1.
That said, I think the same calculations would probably still work if you allowed for v(i) to be greater than 1 — i.e., allowed actors to prefer some distant civilization’s values over their own civilization’s values.
Roughly: I will be looking at when the conditions under which we’d prefer to benefit a random distant civilization by 1 unit vs. benefit our own values by x units, for some x<1. The following sections will be more precise about what that means.
How much more do we care about this if we do ECL with distant evolved species?
Without ECL
Let’s start with establishing a baseline where we ignore ECL. When I talk about our values and choices in this sub-section, I’m not yet taking ECL into account.
Let’s say that we’re faced with the following two options:
We can benefit our own universe-wide values by x units.
We can benefit a random civilization’s values by 1 unit.
Here’s a question you might ask: What does it mean to benefit different values by “1 unit”? Does that require intertheoretic utility comparisons?
In this section, we don’t yet have to worry about that! By assumption, we only care about benefitting distant civilizations insofar as our values overlap with theirs.
This means that we can approach the problem as follows. A random civilization i’s values have v(i) overlap with our values. So the total value of “benefit a random civilization’s values by 1 unit” is proportional to the average v(i) among all civilizations. So the total value of this option is:
This number (the average value-overlap with a random civilizations) will come in handy later, so let’s name it
The first option was to benefit our own values by x units, which is worth x.
Thus, we should prefer to benefit ourselves if and only if x > f. (Where the value of f will be somewhere between 0 and 1.
With ECL
Now let’s see how this changes when we introduce ECL.
As above, let’s say that we can choose between either benefitting a random civilization’s values by 1 unit or benefitting our own values by x units. Here’s the core new dynamic: Our decision to benefit other civilizations is evidence that other civilizations, in an analogous situation, will also choose to benefit other civilizations. Potentially including ours.
For each civilization that is in an analogous situation, we want some metric for how much acausal influence we have on their decision. I’m going to denote our acausal influence over civilization i as c(i). The meaning of this is as follows: If we take a particular action, then there is a probability c(i) that actors in civilization i take their analogous action. (Otherwise, their behavior is independent from our behavior.) If a civilization i has no analogous action, we will say that c(i) = 0.
Now, we still need to make some assumptions about these distant civilizations’ options. As a simplifying assumption, I will assume:
That the decision that is analogous to our “benefit our own values by x units” is for them to benefit their own values by x units.
What does “benefit their own values by x units” mean here? The only relevant implication for my calculations is that we value civilization i’s choice to benefit themselves as worth x*v(i).
That the decision that is analogous to our “benefit a random civilization’s values by 1 unit” is for them to benefit a random civilization’s values by 1 unit.
Just as above: The only relevant implication for my calculation is that we value civilization i’s choice to benefit a random civilization as worth f. (Just as we valued our own decision to do so at f, before we took ECL into account.)
How substantive of an assumption is this?
In the above bullet points, I emphasized that the main calculation-relevant assumption that I’m making is that we value civilization i’s first option as x*v(i), and second option as f. But in order for it to be plausible that these are actually analogous actions (justifying c(i)>0), we need these other civilizations to have a similar relationship to these options as we do.
So for example: Maybe the interventions I’m thinking about is “prioritize making AI aligned to our values slightly higher”3 vs. “prioritize making AIs more cooperative with distant civilizations slightly higher”. If so “x” reflects the relative value that we place on alignment vs. having there be more cooperative AIs in the universe.
Maybe other civilizations face that same decision: If other civilizations are also choosing how highly to prioritize cooperation vs. alignment, and their own version of “x” is similar, then that seems like an analogous decision.
Or maybe other civilizations face quite different options: As long as other actors are choosing between benefitting a broad variety of values vs. just their own values, and are conducting similar calculations, it’s plausible that their decisions could be sufficiently analogous.
Ultimately, I feel like this assumption is a bit shaky, but ok for a first-pass analysis. I think it roughly corresponds to an assumption that other civilizations would appreciate our intervention that “benefits other civilizations broadly” about as much as we would appreciate others doing it — and that our opportunity to benefit others isn’t abnormally high or low.
(I’ll give some further remarks on this below.)
Now, let’s re-consider our above decision, taking ECL into account. If we had to choose between an intervention that benefitted us by x units or benefitted a random civilization’s values by 1 unit — which should we prefer?
If we benefit our own values by x units, then that suggests that each civilization i has an additional probability c(i) of analogously benefiting themselves by x units. We value this at v(i)x. So the total value of this is:
If we instead benefit a random civilization by 1 unit, then each civilization i has an additional probability c(i) of benefitting a random civilization. As we calculated in the previous section, the value of benefitting a random civilization by 1 unit is f. So the total value of this is
Thus, we should choose to benefit our own civilization over a random civilization iff:
Answering the original question
Remember, the question I wanted to study in this setting was:
How much does ECL raise the importance of interventions that broadly benefit a variety of beneficiaries with different values, compared to interventions that mainly benefit our own values?
In the section Without ECL, I wrote that we should benefit our own values iff we could benefit them by more than f — and otherwise choose to benefit random civilizations’ values. This corresponds to valuing benefits to random civilizations at f times as much as benefits to our own values.
In the section With ECL, I wrote that we should benefit our own values iff we could benefit them by more than
— and otherwise prioritize benefitting random civilizations. This corresponds to valuing benefits to random civilizations’ values at
times as much as benefits to our own values. As long as all v(i) is less than 1, this latter value will be larger, meaning that we should be more inclined to benefit others’ values.
The ratio between these, i.e. the degree to which ECL compels us to increase the valuation of “benefit a random civilization’s values” (compared to benefitting our own values) is:
In the numerator, we have all the civilizations that we can acausally influence. In the denominator, we have the civilizations that we can acausally influence weighted by how much our values overlap.
That’s a fine way to think about things. But we can also rewrite it as:
Where we can see that ECL raises the importance of these interventions in proportion to 1 plus the ratio of the acausal influence we have on civilizations that we don’t share values with vs. civilizations that we do share values with.
What are plausible values for these numbers?
This section will contain some pretty wild guesses. I wouldn’t encourage anyone to take these numbers too seriously, but I figured it could be good to gesture at how you could approach this, and roughly what the order of magnitude might be.
First: I’ve been generally talking about benefiting civilizations’ universe-wide values. What about civilizations that have purely local preferences? It’s not clear how to count them. Fortunately, this doesn’t matter for the above formula. We probably don’t have any relevant acausal influence on those civilizations (since the reason that we’re reasoning about ECL is to benefit our universe-wide preferences, and they have no analogous reason). This means that c(i) is 0, so they don’t appear in either the numerator nor the denominator of the above formulas.
Second: What about distant civilizations that are controlled by misaligned AI? In this section, I’ll assume that we are not correlated with misaligned AI in any relevant way, and thereby ignore them. (Just as the civilizations with local preferences, in the above paragraph.) I’ll talk more about the misaligned AIs in the next section.
(Incidentally: This pattern (that our formula isn’t sensitive to the existence of civilizations that we can’t acausally influence) makes me feel better about the assumptions in With ECL. Even if our decision isn’t analogous to many other civilizations’ decisions — that doesn’t necessarily matter for the bottom-line.)
With that out of the way, let’s slightly rewrite the above expression. Remember, just previously, I derived that the degree to which ECL increases the value of “benefitting a random civilization’s values” (compared to just benefitting our own) was equal to:
Now, let’s define a as the average acausal influence we have on civilizations weighted by our overlap in values with them:
Using a, we can rewrite the denominator as
Second, let’s define b as the reverse of a: the average amount that we correlate with civilizations weighted by our lack of overlap in values with them:
Using b, we can rewrite the numerator as
We can then rewrite the above expression as:
(Side-note: Remember how we previously divided by f, in order to get a number for how much more interested we become in these interventions, after taking ECL into account? If we undo that after the above simplifications, we get that you should benefit your own civilizations by x units whenever:
I.e., intrinsically caring about others’ values (f) is roughly additive with ECL-reasons to do so (b/a). Just from this, we can conclude that if you intrinsically care about aliens’ values a lot, ECL probably won’t further increase this. But if you intrinsically care very little, then ECL could multiplicatively increase how much you care by a large amount.)
This lets us separately estimate (1-f)/f and b/a. Let’s make up some numbers!
On how large f, i.e., the average value overlap between us and a random other civilization, is.
Remember that we’re excluding civilizations with local values, and civilizations headed by misaligned AIs.
Among universe-wide values, I’m uncertain whether I’ll end up with fairly simple values (e.g. some variant of hedonistic utilitarianism, where pleasure is a fairly simple thing) or some very complex values (that depend on a lot of contingencies of our evolutionary history).
Let’s say I’m ⅓ on the former and ⅔ on the latter.
Let’s say that if I end up with some fairly simple values, I think that… ⅓ of evolved civilizations’ universe-wide values appeal to the same thing.
And if I end up with fairly complex values, I end up valuing benefits to distant evolved civilizations at… 10% of my own.
And let’s say that I’m happy to just take the expectation over these two possibilities. (Which is by no means obvious when you have moral uncertainty.)
→ f = ⅓ * ⅓ + ⅔ * 10% ~= 18%.
How large might b/a be? I.e., how much less do we correlate with civilizations that don’t share our values than civilizations that do share our values, on average? (Again: Excluding civilizations with local values, and civilizations headed by misaligned AI.)
Here, I feel pretty clueless. Let’s say 3x less. Meaning that b/a~=⅓.
(For some other people’s discussion of that question, see section 3.1 of Oesterheld (2017) and this blogpost.)
So that would suggest that ECL increases the value of helping distant civilizations by roughly
Obviously those numbers were terrible. If I thought a lot more about this, I suspect that I’d end up thinking that ECL made these sorts of interventions somewhere around 1.5x-10x as important as they would have been without ECL.
How much more do we care about this goal if we also do ECL with distant AI?
I don’t think this changes the calculus much, because:
I think the total number of civilizations controlled by misaligned AIs are not (in expectation) significantly larger than the number of civilizations with values that come from evolved species.
But I think the argument for ECL-cooperation with misaligned AIs are less strong than the corresponding arguments for cooperating with evolved pre-AGI civilizations.5 (I discuss this more in Are our choices analogous to AI choices?)
So ECL with AI merely adds a group that’s similarly-large to the group that we already cared about, but that we have less reason to do ECL-cooperation with. In which case it won’t more than double the value of these interventions.
I still think that doing ECL with distant, misaligned AIs might be important! I just think it has a negligible impact on how much we care about benefiting distant, random civilizations. For content of what I think might matter more, here, see my next post on ECL with AI.
What about completely different actors?
What about civilizations that don’t fit into my picture of either “evolved species” or “misaligned AI”? The universe could be strange and diverse place — why would I limit myself to these two categories that happen to be salient to me right now?
Good question! This feels tricky, but here are some thoughts:
The distinction feels at least somewhat natural to me. Abstractly: First you have some intelligent creatures that evolve through natural selection, and then they design some other intelligent creatures, which may or may not share their goals. It doesn’t feel like I’m appealing to something super contingent.
If parts of the multiverse work very differently, but there aren’t many cases where our parts of the multiverse or their part of the multiverse try to benefit or harm each other, I don’t think that matters much. The situation is very similar to if we were alone.
What could matter is if a big majority of the positive effects from intervening on misaligned AI came via the route of positively influencing these strange and inscrutable parts of the universe. If that was the case, my calculations here would be missing most of the story, and so wouldn’t be very informative.
Which is enough for e.g. ECL to incentivize them to benefit those distant civilizations.
To do this properly, we should probably define some measure over an infinite number of possible civilizations. I think the rest of the math would still hold.
Which disproportionately benefits our own values, even though it would also affect other values. If nothing else, it will influence the degree to which Earth-origination civilization is cooperative or not.
How is the benefit to our own civilization, counted here? Well, we could put it somewhere there in the sum, with c(i)=1 and v(i)=1. But for sufficiently large N, it will be negligible.
This is talking about the current state of arguments. I think it’s plausible that I would, on reflection, believe that it was similarly reasonable to do ECL with misaligned AI as with evolved pre-AGI civilizations. But aggregating over my uncertainty, I’m currently more inclined to cooperate with evolved pre-AGI civilizations.

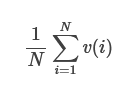









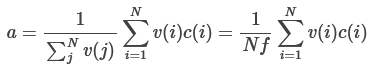
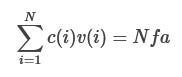
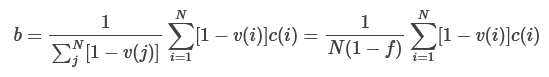




> (For some other people’s discussion of that question, see section 3.1 of Oesterheld (2017) and this blogpost.)
I'm confused why you've cited the "Three wagers" blogpost. The "wager in favor of higher correlations" isn't a wager in favor of high correlations with agents with _different values_, relative to those with the same values. The wager is in favor of acting as if you correlate with agents who aren't exact copies, but (as Treutlein himself notes) such agents could still strongly share your values. So in practice this wager doesn't seem to recommend actions different from just fulfilling your own values.