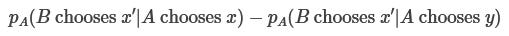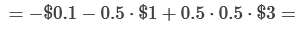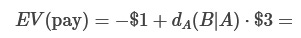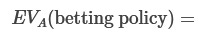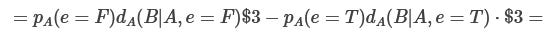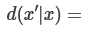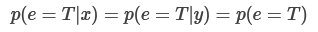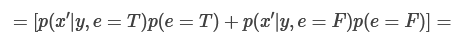When does EDT seek evidence about correlations?
Informal summary
The algorithm that EDT chooses to self-modify to is known as “son-of-EDT”. I argue that son-of-EDT doesn’t do direct-entanglement-style-cooperation with its new correlations, but does try to benefit the people who its parent was correlated with when it made the self-modification.
In addition, son-of-EDT will be interested in gathering more evidence about who the parent was and wasn’t correlated with, at the time of making the decision, and change who it tries to benefit based on what it learns.
In cases where potentially-correlated agents can gather evidence that makes their estimates about correlation converge, I think evidence-seeking works in a fairly commonsensical way. For example, they will pay for evidence that tells them whether their correlations are sufficiently high to make an acausal deal worthwhile. (As long as the evidence is sufficiently cheap, and the evidence could flip them from thinking that the deal is worth-it to thinking it’s not worth it, or vice versa.)
Updating on some types of evidence would predictably lead actors to estimate very small correlations with other agents. This is not true for any of the examples of “evidence” for which I argue that agents want to seek out that evidence, in this post. Instead, the relevant evidence has the property that it preserves expected acausal influence, i.e., updating on the evidence can change estimated correlations, but it doesn’t systematically increase or decrease it.
I will now introduce a “no prediction”-assumption (that the post will assume) and some notation. Then I will offer a more formal summary.
“No prediction” assumption
In a 1-shot prisoner’s dilemma, there are two different ways in which two agents can achieve cooperation by acausal means:
You might think that you are similar to your counterpart, and choose to cooperate because that means that they’re more likely to cooperate (due to a similar argument).
You might think that your counterpart is predicting what you do, and that if you cooperate, they will infer that you cooperated. And that this inference will make them more likely to cooperate, in response.1
In this post, I want to ignore the latter kind. To facilitate that, I will make the following simplifying assumption:
For every pair of agents Alice and Bob (A,B), there is nothing that Alice can do to affect Bob’s beliefs about Alice, other than her acausal influence on a single choice that Bob is making. More formally:
For every observation O that Bob can make other than observing what choice he made in a particular dilemma (and events that are causally downstream of that choice), and for every pair of actions (X,Y) that Alice can take, we have:
(Where pA is Alice’s prior.)
“No prediction” assumption might be a slightly misleading name, here. I also want to exclude observations of an agent’s action — or indeed, any kind of observation that would correlate with an agent’s action. (According to that agent.)
Supplementing the “no prediction” assumption, I assume that the only source of correlation between agents’ decisions is that the agents believe that they might be following similar algorithms, and thereby are likely to take analogous actions. (I.e., my results would probably not hold for arbitrary priors with unjustified correlations in them.)
Notation
When an agent A is thinking about affecting another agent B, they care about changing the probability that B does something. For example:
(The subscript A signifies that these are probabilities according to A’s prior.)
As shorthand for this, let’s use dA(B chooses x’ | A chooses x), where the d stands for difference.
In some situations, A and B are in sufficiently similar epistemic positions that each of A’s actions x clearly corresponds to one of B’s actions x’, and for each such pair (x, x’), it is the case that dA(B does x’ | A does x) is equally large. If this is the case, we’ll abbreviate those values as dA(B|A). (A's belief about how much A doing something increases the chance that B does his analogous thing, which will be a number between 0 and 1.)
Rather than just using A’s prior pA, I will sometimes be interested in what A’s prior says about correlations after being conditioned on some evidence e, i.e.:
I will abbreviate this as dA(B chooses x’ | A chooses x, e) or (if each of A’s actions clearly correspond to one of B’s actions) as dA(B|A,e).
More formal summary
In the first section of this summary, I will be conflating Alice’s perceived acausal influence on Bob and Bob’s perceived acausal influence on Alice. All my claims are not necessarily true unless dA(B|A) = dB(A|B). In the second section of this summary, I correct this assumption.
When does EDT seek evidence about correlations?
Consider Alice, who cares about her correlation with Bob. Let’s say that Alice is initially uncertain whether evidence e will turn out to be equal to true or false. (For example, whether it is true that “Wikipedia says that Bob used to be a lumberjack”.) She observes it, and it turns out that it’s true. This may change her correlations with Bob. What does that mean, more precisely?
Let’s use “A1” to refer to Alice in step 1, before observing evidence, and let's say she has two options: action X1 or action Y1. Then, in time step 1, Alice’s perceived influence on Bob was:
(I’m just using “A” for the prior pA, because all time-slices of Alice have a shared prior.)
Let’s say that A1 selects action X1, and that X1 is a choice to look at some evidence. Let’s use “A2T” to refer to Alice in time-step 2 who has observed that Alice chose X1 and has observed e to be true.2 And let’s say she can choose action X2 or action Y2. In time step 2, after observing evidence E to be equal to true, we can now write Alice’s perceived acausal influence on Bob as:
Notice that multiple things have changed!
We now conditioned on being in the world where e=T.
We now conditioned on the knowledge that A1 chose X1.
We have switched from consider the conditional difference between “A1 does [X1 or Y1]” to “A2T does [X2 or Y2]”.
But these need not necessarily go together. Alice’s prior pA can also provide well-defined values for:
and
(In the first row — note that I don’t condition on the observation that A1 chose X1 in both terms (like I did in A2T’s choice above). If I did, the second term would condition on a probability 0 event.)
Here are all those quantities in a table:
Updateful EDT can only make decisions on the basis of diagonals. But we need not constrain ourselves to updateful EDT. If Alice at time-step 1 has significant control over how her successor will act at time-step 2, we can investigate which of these quantities she would prefer that her successor bases her decision on.
In this post I will argue that:
If A1 is an EDT agent, and assuming the “No prediction” assumption, A1 will want her successor A2 to benefit agents that A1 correlates with. Not necessarily agents that A2 correlates with.
This means that son-of-EDT will:
not optimize expected utility by the light of A1’s prior (i.e. pick argmaxx(EA(U|A2 picks x)), and
not particularly care about either dA(B|A2T) or the corresponding quantity after updating on evidence.
(Saliently, this means that son-of-EDT is not (the most natural interpretation of) “updateless EDT”. Since the most natural interpretation of updateless EDT would maximize expected utility by the light of A1’s prior.)
This is argued in 1. Son-of-EDT cooperates using its parent’s entanglements.
If A1 is an EDT agent, and assuming the “No prediction” assumption, A1 will want her successor A2 to gather evidence about who A1 was correlated with at the time of choosing her successor.
This means that A1 would want A2 to learn about dA(B|A1,e=T). (And make decisions that benefitted agents that A1 correlated with at time-step 1, according to that formula.)
Well… at least that’s true given the assumption of symmetric acausal influence, that I mentioned at the start of the summary. But let’s now poke holes in that assumption.
Asymmetric acasual influence
When doing this, we will not need separate time-steps. But we will need a third actor. Our agents will now be Alice, Bob, and Carol.
If we allow for asymmetric acausal influence, we can construct scenarios where Alice perceives herself as having acausal influence on Bob, Bob perceives himself as having acausal influence on Carol, and Carol perceives herself as having acausal influence on Alice. (But not the other way around.)
You may doubt that such asymmetries are ever reasonable. For an example where this appears naturally, see Asymmetric beliefs about acausal influence.
In this post, I will argue that:
If Alice, Bob, and Carol are in a circle where they can each acausally influence the agent to their left, then they will all be incentivized to benefit the agent to their right.
In short: This is because they all stand to the right of the agent that they can acausally influence — and so they want to acausally influence that agent to benefit their right.
Generalizing (and assuming the “No prediction” assumption):
If an agent doesn't perceive themselves as being able to acausally influence you, then you probably have no acausal reason to benefit them.
If an agent perceives themselves as being able to acausally influence you, then that might incentivize you to benefit them.
Though I think you only have reason to benefit them if there is some closed circle of actors (potentially just two) who think they are able to acausally influence the next person in the circle.3
This is argued in 3. EDT recommends benefitting agents who think they can influence you.
Taking this into account, we can now refine the last bolded statement from the above section into:
If A1 is an EDT agent, and assuming the “No prediction” assumption, A1 will want her successor A2 to gather evidence about who could acausally influence A1.
This is argued in 4. EDT recommends seeking evidence about who thinks they can influence you.
I.e., A1 will be interested in evidence e that affects dB(A1|B,e) or dC(A1|C,e).
Two caveats on this are:
A1 would not want her successor to condition on what A1 chose to do, when estimating these quantities. That would predictably destroy Bob’s and Carol’s perceived influence over A1’s choice. (I discuss this more in What evidence to update on?)
The “No prediction” assumption is crucial here. Without that, I suspect there would be a lot more caveats like the above bullet point.
Other sections
Those are the core conclusions of the post. In the remaining sections:
I apply the above framework to Fully symmetrical cases and cases with Symmetric ground-truth, different starting beliefs — and conclude that people seem to gather evidence in a fairly common-sensical way.
In particular: They will always pay for sufficiently cheap evidence that will reveal whether they do or don’t have sufficiently large acausal influence to make a deal worthwhile.
Then I have some appendices on:
A market analogy for some of the results, where it looks like “A thinks they can influence B” is analogous to “A wants to buy B’s goods”.
1. Son-of-EDT does not cooperate based on its own correlations
“Son-of-EDT” is the agent that EDT would self-modify into.
Consider the following case:
Alice and Bob are choosing successor-agents. The successor agents will then play a prisoner’s dilemma where they can pay $1 to send the other $10.
Both Alice and Bob have two different options:
Deploy defect-bot, which will defect in the prisoner’s dilemma.
Deploy an agent that I will call “UEDT” (short for “updateless EDT”).
Alice’s UEDT agent UEDTA would…
Compute:
EA(utilityA | UEDTA selects cooperate)
EA(utilityA | UEDTA selects defect)
…using Alice’s prior probability distribution and utility function…
…and pick the option with the highest expected utility.
Bob’s UEDT agent would do the corresponding thing.
Alice’s and Bob’s prior probability distributions both imply that UEDTA will almost certainly take the same action as UEDTB.
The “No prediction” assumption holds. Neither Alice, Bob, nor their successors will observe anything about their counterparts’ choices.
Alice follows EDT. She believes:
That her choice about successor-agent does not give her evidence about Bob’s choice, nor about the choice of any successor-agent.
That Bob has a 50% chance of deploying UEDTB and 50% chance of deploying defect-bot.
What will Alice choose?
If Alice chooses to deploy UEDTA…
Then UEDTA will cooperate.
This is because there’s a 50% chance that Bob deployed UEDTB, and so EA(utilityA | UEDTA selects cooperate)~= -$1 + 50% * $10 > $0.
And EA(utilityA | UEDTA selects defect) ~= $0, since both defect-bot and UEDTB are likely to defect if UEDTA defects.
If Alice chooses to deploy defect-bot, then it will defect.
Since Alice (by assumption) does not believe that her choice of successor-agent can affect what successor Bob deploys, or what action Bob’s successor chooses, it is strictly better to deploy an agent that defects than an agent that cooperates. So Alice will deploy defect-bot.
So in this example, EDT does not want its successor to acausally cooperate using their own correlations. If the parent is not correlated with someone, then they do not want their successor to needlessly benefit that agent.
I suspect that this generalizes. I expect that EDT would want its successor to acausally cooperate based on its parent’s correlations, and not based on its own correlations.
This is for the case of cooperation via “direct” entanglement. If agents can observe and predict each other, the story can get more complicated. (In the above, deploying UEDT would be much better than defect-bot if both agents could see what the other deployed.)
2. Asymmetric beliefs about acausal influence
EDT agents will sometimes have asymmetric beliefs about their acausal influence on each other, in a way that isn’t easily explainable by one of them making a mistake.
Here’s an example of a case where you’d expect asymmetric beliefs about entanglement, for updateful agents:
Alice, Bob, and Carol are arranged in a circle.
Each of them will get the opportunity to pay $1 to send $10 to the actor immediately to the right of them in the circle.
But before they make that decision, they will learn whether the actor to the right of them paid $1 to send $10 to their right.
(This is an exception to the “No prediction” assumption, that I otherwise make in this post.)
In order to get things started, a random actor will be selected and have a 50/50 chance of being told that the immediately preceding actor did or did not send $10.
This structure is common knowledge among all actors.
The figure assumes that actors are facing inwards.
Let’s assume that Alice, Bob, and Carol initially would think of themselves as fairly correlated with each other, while still having notable uncertainty about what the others will do. If so, the structure of observations in the circle will mean that all agents see themselves as having substantial acausal influence on the agent to their left, but little acausal influence on the agent to their right. This is because they will already have observed significant evidence about what the agent to their right chose, but they won’t have observed any evidence about the agent to their left.
(This effect is attenuated by the necessity of selecting a random start-point — which means that there is a ⅓ chance that you are not observing the action of the agent to the right. If we wanted to reduce that effect, we could make the circle much larger, to push this probability down.)
In this case, updateful EDT may well want to benefit the agent to their right, despite how little acausal influence they will have on that agent. Indeed, when calculating the value of that, it doesn’t matter how much or little acausal influence the EDT agents have on their right-hand agent. The only thing that matters is how much acausal influence they have on the agent to their left. When Alice decides whether to benefit Carol, she only cares about whether this is evidence that Bob will benefit Alice.4 (Since Bob is the only agent who can benefit Alice.)
This illustrates two things:
It’s possible for agents to find themselves in situations where Alice reasonably perceives herself as having more influence on Bob than Bob perceives himself to have on Alice.5
In at least one scenario where this happens, agents like Alice will want to benefit Carol, who perceives herself as being able to acausally influence Alice — even if Alice doesn’t perceive herself as being able to acausally influence Carol.
Let’s now consider a decision problem that supports a generalization of that last bullet point.
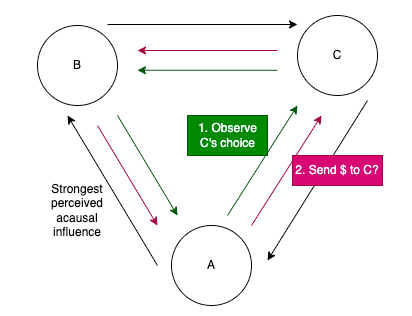
3. EDT recommends benefitting agents who think they can influence you
Consider the following situation:
There are 3 agents: Alice, Bob, and Carol.
Alice has two buttons in front of her. One sends $3 to Bob and one sends $3 to Carol. Each button costs $1 to press. She can choose to press both.
Bob has analogous buttons for sending money to Alice and Carol.
Carol has analogous buttons for sending money to Alice and Bob.
Alice believes that she has a lot of acausal influence on Bob, but little on Carol.
Bob believes that he has a lot of acausal influence on Carol, but little on Alice.
Carol believes that she has a lot of acausal influence on Alice, but little on Bob.
To give some precise numbers, let’s say that d(B|A)=d(C|A)=d(A|C)=0.5, and d(A|B)=d(B|C)=d(C|A)=0.
(For the purposes of this post, it doesn’t matter why they have this set of beliefs. But a similar set of beliefs could perhaps be explained by Alice already having received some evidence about Carol’s action; Bob having received evidence about Alice’s action; and Carol having received evidence about Bob’s action; as in the dilemma outlined in 2. Asymmetric beliefs about acausal influence.)
What will Alice do in this situation?
If Alice sends $3 to Bob, that’s a lot of evidence that Bob sends $3 to Carol. This isn’t worth anything to Alice.
But if Alice sends $3 to Carol, that’s a lot of evidence that Bob sends $3 to Alice.
More precisely:
So everyone in the circle will send money to the person who can acausally influence them — not the person who they can acausally influence.
I think this generalizes to larger-scale cases. Intuitively: If Alice thinks she can acausally influence Bob, she wants to take actions that make her think that Bob will benefit her. That means that she wants Bob to take actions that help people who think they can influence Bob. Accordingly, Alice will help people who think they can influence Alice.
Quick remark: This is analogous to other principles in similar problems, like:
Alice won’t necessarily help people who have good opportunities to help Alice. But Alice will preferentially help people who she has good opportunities to help.
Alice won’t necessarily help people who she thinks have a lot of power. But Alice will preferentially help people who think that Alice has a lot of power.6
(More on this in A market analogy.)
If that didn’t make any sense, that’s ok!
Also, the patterns of “who can influence who?” that will allow for this type of one-sided influence are very similar to the patterns of “who can benefit who?” that enable ECL when only some agents are able to benefit each other. This latter question is discussed in section 2.9 of Oesterheld (2017). In short: You need either a circle of people who can (potentially) influence/benefit each other, or an infinite line.
4. EDT recommends seeking evidence about who thinks they can influence you
Let’s now turn to a variant of the same scenario, where Alice, Bob, and Carol get the option to gather evidence about their degree of acausal influence.
Each agent gets 3 additional buttons, marked a, b, and c. They all cost $0.01 to press, and the intuitive purpose of buttons a, b, and c is to give agents information about whether they have acausal influence over others or not. Informally: If an agent presses button a, then they will learn whether Alice has 100% or 0% acausal influence over Bob according to Alice’s prior — and correspondingly for button b and Bob; and for button c and Carol.
To analyze this scenario, I will assume that each of Alice, Bob, and Carol first commits to a full policy, which specifies:
Which (of any) buttons a, b, c they will choose to press.
For every possible combination of results:
Whether they will pay to send money to the other agents.
Here’s a more precise description of what the buttons do:
There are 3 unknown facts about the world, which the buttons will reveal.
Either a=T or a=F. (T and F stands for True and False.)
Each agent is 50/50 on which one it is.
If you press button a, you learn whether it is the case that a=T or a=F.
Likewise for the other buttons.
(The probabilities that a is true, b is true, and c is true are uncorrelated.)
Intuitively, we want:
If a=T, then dA(B|A)=1.
If a=F, then dA(B|A)=0.
We get this if Alice’s prior belief has the following properties:
By definition,
d(B|A)= (pA(B chooses x’ | A chooses x) - pA(B chooses x’ | A chooses y)).By previous assumption, this is equal to 0.5.
But if we also condition on a=T, we have:
pA(B chooses x’ | A chooses x, a=T) = 1.
pA(B chooses x’ | A chooses y, a=T) = 0.
pA(B chooses x’ | A chooses x, a=F) = pA(B chooses x’ | A chooses y, a=F)
In other words, if a is true, A has total acausal influence over B. If a is false, A has no acausal influence over B.
So dA(B|A,a=T)=1 and dA(B|A,a=F)=0.
Bob’s and Carol’s beliefs have analogous properties with respect to button b and button c.
Recall the discussion about evidence in the More formal summary. Given a prior, I introduced a distinction between:
The correlation that a successor agent would have with others, after seeing the evidence: dA(B|A2T,e=T).
The correlation that the original agent would have with others, if we just condition that agent’s prior on the evidence: dA(B|A1,e=T).
In the current scenario, the buttons are supposed to provide evidence about the original agents’ correlation with others (i.e., the analog of the second of the above quantities: dA(B|A1,e=T)). I will not pay any attention to any successor agent’s correlation with other agents. (Since, according to 1. Son-of-EDT cooperates using its parent’s entanglements, this isn’t particularly relevant when agents have sufficient ability to commit to certain policies.)
In the decision problem sketched about — what will Alice do?
As before, she has the option of just sending money to Carol. As before, the expected utility of this is 0.5.
She could condition this on actually having acausal influence over Bob. After all, acausal influence on Bob is the only reason she’s doing this.
But if Alice does that, Bob is more likely to condition his decision on having influence over Carol. (I.e., on b=T.)
In expectation, Alice saves an expected $0.5 by not having to send money if she can’t influence Bob.
But if she influences Bob to choose the same policy as her, Bob has a 50% chance of discovering that b=F (i.e. to update that he can’t influence Carol), and then not sending any money to Alice. So in expectation, Bob sends Alice half as much money as he did in the unconditional case: $0.75 instead of $1.5.
(The full calculation here is that Alice only thinks she influences Bob in worlds a=T, and in addition, Bob, only sends money in worlds where b=T. Since these events are independent, Alice’s winnings are 0.50.55=$0.75.)
Alice’s payment and Alice’s winnings have both been halved: Which is a bad deal, since the winnings were larger than the payments.
But instead, she could condition on being in a world where Carol would see herself as having acausal influence over Alice, i.e. only send money if c=T.
To calculate the EV of this, let’s consider two different worlds: The one where a=T and the one where a=F.
Alice never learns which one she’s in, so in both worlds, Alice pays $0.1 for the button and in expectation sends p(c=T)*$1=$0.5 to Carol.
If a=F, then Alice will have no further effect on Bob.
If a=T, it is both the case that Bob will follow the same policy and that he’ll find that a=T and send the money.
Similar to the above case, Alice saves $0.5 from not having to send money if c=F. But this time the risk that Bob doesn’t send money doesn’t apply — because if she influenced Bob, then Bob will find that a=T.
So EDT recommends that you investigate whether anyone would think themselves able to influence you, if they knew more about the world. And then help people only insofar as this is the case.
Intuitively, we can appeal to a similar intuition as above. If Alice thinks she can acausally influence Bob, she wants to take actions that make her think that Bob will benefit her. There’s no reason for why she’d want Bob’s help to be conditional on Bob being able to influence someone else. Alice doesn’t care about that! But Alice is ok with [her action acausally influencing Bob to follow a policy that] only helps Alice in worlds where she actually thinks she can influence Bob. The other worlds don’t matter, as she judges her action to have no acausal influence in those worlds.7
I think this generalizes to much larger and more complicated cases. I.e., I’d speculate that:
If multiple people think they might be able to influence you, then you should investigate their cruxes and prioritize people for whom the cruxes came up positively.
If you can only gain a little bit of evidence about whether others would think themselves able to influence you, then it’s still good to get that and to slightly adjust the bar at which you’d help them.
You never care about figuring out who you can acausally influence, except insofar as this is related to other things, such as who can acausally influence you.
I think this only holds if the “No prediction” assumption holds. For example, I think you probably care about figuring out whether Omega is a good predictor in Newcomb’s problem.
Nevertheless, this conclusion is quite wild to me! Does it suggest that we should just go with our first instinct about “who can I acausally influence?”, use that to determine how interested we should be in acausal trade, and then never ponder that question again? I don’t think that summary is quite right (at least not in spirit) but it’s certainly closer to the truth than I expected.
I am somewhat reassured by the commonsensical results in 6. Fully symmetrical cases and 7. Symmetric ground truth, different starting beliefs.
Also, the appendix A market analogy gives some intuition for what’s going on, that’s helpful to me.
That said, I still feel puzzled about this, and would appreciate more insight on it.
I should flag one thing: It’s not good to update on every piece of evidence. In particular, if Alice were to update Carol's prior pC on Alice’s own choice of what to do, then that would suggest that Carol has no acausal influence on Alice’s choice. (Because Alice’s choice would be fixed.) It seems quite tricky to determine what sort of evidence is good vs. bad to update on in general, but given the “No prediction” assumption, I think it’s fine to update on anything except for your own action, and events that are causally downstream of that. I explain why in the appendix What evidence to update on?
5. Interlude: What kind of evidence is this?
You might find yourself asking: What are these mysterious buttons doing? How could they provide evidence about how much acausal influence these agents have?
One thing to note is that the concept of “evidence about correlations” can be fully captured by certain correlational structures in the agent’s Bayesian priors. And updating on that evidence can be captured by normal Bayesian updating: pA(B chooses x’ | A chooses x, a=T) is higher than pA(B chooses x’ | A chooses x, a=F). So this is “evidence” in the normal, Bayesian sense.
But why would those correlational structures be there in the first place? What structures in the world do the buttons correspond to? I’ll give two different examples.
Firstly, a relatively prosaic example. Alice might be confident that her decision correlates with certain algorithms, and confident that her decision doesn’t correlate with certain other algorithms. She might be uncertain about which of these algorithms Bob implements. Button “a” might give her information about whether Bob uses an algorithm that is similar to her own, or whether Bob uses an algorithm that is very different.
Secondly, a relatively less prosaic example. Alice might be philosophically confused about the nature of correlation. In some sense, she might have access to all the information about her own and Bob’s algorithm that she’s going to get. But she doesn’t understand what’s the best way to go from there to assigning the conditional probabilities that specify d(B|A). In this case, we could say that “a=T” is true iff Alice would (on reflection) conclude that the conditional probabilities are high, and “a=F” if she would (on reflection) conclude that the conditional probabilities are low.8
Note that this latter case could conform to the same correlational structure as the relatively more prosaic case. pA(B chooses x’ | A chooses x, a=T) is higher than pA(B chooses x’ | A chooses x, a=F), because if Alice on-reflection thinks that A and B are very correlated, then it’s very likely that B chooses x’ if A chooses x.
However, this latter case does not appeal to empirical uncertainty. At best, it appeals to logical uncertainty, which tends to cause all kinds of problems for Bayesian approaches to uncertainty. (Or even worse, it might appeal to philosophical uncertainty, which isn’t captured by even those formal methods we do have for logical uncertainty, such as logical induction.) So if you dug into this latter case further (and similar cases) you would predictably encounter all kinds of strange issues.
6. Fully symmetrical cases
In symmetric cases, I think the lessons from 4. EDT recommends seeking evidence about who thinks they can influence you accord well with common sense. If Alice and Bob have the same beliefs about acausal influence, have the same opportunities for investigation, and have the same opportunities to help each other — then they’re both interested in finding out whether their correlation is large enough to justify cooperation.
Consider the following case:
A prisoner’s dilemma between Alice and Bob, where each can pay $1 to send the other $3.
Each of them have access to their own copy of a button e that will give some evidence about their acausal influence over each other. They both agree that
They share a prior p(e=T) that button e shows “True”. So at the start:
Assume that the cost of pressing button e is eps. (For epsilon.)
The value of conditional paying is:
For every p(e=T) > 0, there’s an eps that’s small enough that this expected value is positive (i.e., higher than doing nothing).
This is true for dA(B|A,e=T)=0.5, and more generally, whenever the deal would be worth it if e=T, i.e. when dA(B|A,e=T)$3 > $1.
The value of unconditional paying is:
The last term (starting with p(e=T)) appears in both EV(pay) and EV(press e, pay iff e=T).
For every p(e=T)<1, the first term (starting with p(e=F)) is negative.
This is true for dA(B|A,e=F)=0.1, and more generally, whenever the deal wouldn't be worth it if e=F, i.e. when dA(B|A,e=F)$3 < $1.
Thus, for every p(e=T) < 1, there’s an eps with an absolute value smaller than the first term’s absolute value, for which conditional paying will be higher than the expected value of unconditional paying.
So in symmetrical cases, people will always seek out sufficiently cheap evidence about correlations.
7. Symmetric ground truth, different starting beliefs
You might have the following intuition: People might have asymmetric beliefs about acausal influence right now, but on reflection, in “normal” circumstances, Alice’s perceived influence on Bob would often line up with Bob’s perceived influence on Alice. (It’s unclear what this sense of “on reflection” means.)
In this case, I think the situation is still mostly common-sensical:
Consider a case like the fully symmetrical one above, except Alice’s prior is that pA(e=T)=0.1 and Bob’s prior is that pB(e=T)=0.5.
If the cost of pressing e is eps, and pressing the button is an analogous action despite their difference in credences, then:
For sufficiently small eps, this will be positive EV for both A and B.9 Moreover, for any prior probability of p(e=T) between 0 and 1 that they have, there’s always an eps that is small enough that they both gather the evidence and cooperate.
Different priors lead to betting
However, there’s one strange thing about these cases. If Alice and Bob start out with different priors, they can often both get higher expected value deals by betting on their difference in beliefs. One thing they can bet on is the outcome of pressing e. It turns out that it can actually be a better deal for Bob to send money when e=F than when e=T.
(If this is already obvious to you, feel free to skip the rest.)
Consider changing the above deal so that Bob instead sends money when e=F. (And we stipulate that this is now the “analogous action” to Alice sending money when e=T.)
This will be higher EV for Alice than the non-betting policy!
Meanwhile, it will be the exact same EV for Bob, since Bob thinks e=T and e=F is equally likely.
By adjusting the numbers, we could find cases where the betting policy would be preferred by both Alice and Bob.
This is a bit weird, but we already knew that you can bet on anything, and that betting-happy agents with wrong beliefs will lose their shirts. This is just another thing you can bet about. Nothing new under the sun.
Also, the fact that betting worked in this case relied on Alice and Bob having mutual knowledge about their disagreement, and the disagreement nevertheless persisting — which is not supposed to happen if agents have common priors, according to Aumann’s agreement theorem. I suspect that betting, here, would actually require different priors — and not just having observed different evidence.
Appendices
What evidence to update on?
In section 4. EDT recommends seeking evidence about who thinks they can influence you, my analysis suggested that agents should seek out evidence about who other agents could acausally influence, according to that other agent’s prior. For example, Alice should seek out evidence c such that dC(A|C,c=T) and dC(A|C,c=F) were different from Carol’s prior dC(A|C) — and help Carol iff dC(A|C,c) was high.
But Alice needs to be careful about what evidence she updates on. For example, let’s say that Alice makes a certain choice. Let’s abbreviate “Alice commits to a particular policy [with details that I won’t specify here])” as p. If Alice uses that information to estimate Carol’s acausal influence…
dC(A|C,p) = pC(Alice chooses x’ | Carol chooses x, p) - pC(Alice chooses x’ | Carol chooses y, p)
Now, either Alice’s choice was to choose x’, in which case both terms are equal to 1. Or Alice’s choice was to choose something other than x’, in which case both terms are equal to 0. Regardless, dc(A|C,p) = 0. This suggests that Carol has no influence on Alice’s decision at all.
So apparently, we don’t want Alice to update Carol’s prior on Alice’s own decision, when estimating Carol’s acausal influence! Can we say anything more general about what Alice should or shouldn’t update on?
Given the “No prediction” assumption, my guess is that Alice should be fine with updating Carol’s prior on any information that isn’t causally downstream of Alice’s own action.
Why is this? Well, intuitively, the reason why it must be a bad idea to update on Alice’s own action is that this predictably reduces acausal influence to 0. But for any evidence that isn’t downstream of Alice’s own action, we can show that updating on that evidence will preserve Carol’s expected acausal influence. So it won’t predictably make Alice neglect Carol’s preferences — it will only redistribute in what worlds Alice care more vs. less about them.
Here’s the proof.
Let’s say that Carol’s initial perceived acausal influence over Alice is d(A chooses x’ | C chooses x). There’s a button e that will reveal either e=T or e=F, which Alice is considering pressing.
In order to check that the button won’t systematically reduce Carol’s estimated acausal influence, we can calculate the expected acausal influence that Alice will assign to Carol after pressing the button and conditioning on its value.
Let’s abbreviate:
“A chooses x’ ” as just x’.
“C chooses x” as just x.
“C chooses y” as just y.
I’ll also omit subscripts C from p and d.
Then Carol’s expected acausal influence after conditioning on the button-result is:
In order for the button to preserve acausal influence, we need this expression to equal d(x’|x). So let’s expand d(x’|x) and see when it equals the above expression:
Now, recall the “No prediction” assumption (with some variable-names replaced, to suit our current example):
For every observation [e=T] that [Alice] can make other than [Alice’s] own choice (and events that are causally downstream of Alice’s choice), and for every pair of actions [(x,y)] that Carol can take, we have:
In other words, if the “No prediction” assumption holds, then as long as the evidence e isn’t Alice’s own choice (or something causally downstream of Alice’s choice), then:
If we accordingly substitute the values, then we get:
So given the “No prediction” assumption, Alice can update Carol’s prior on anything that isn’t causally downstream of Alice’s action — and preserve expected acausal influence.
When does updateful EDT avoid information?
Given that we’re talking about updateful EDT agents, each “successor agent” will be an EDT agent who shares values with the parent agent, but who will have different actions available to them, and a strictly larger amount of information. Alice “avoids information” if she strictly prefers an action x1 over an action x2, where x1 and x2 have identical consequences except that her successor agent has strictly less information in x1 than in x2.
(I will neglect reasons that EDT might avoid information that would apply equally to any decision-theory, e.g.: they intrinsically disvalue certain knowledge.)
Here’s a taxonomy of reasons for why Alice might avoid information:
The new information will make Alice’s successor (or correlated agents that share values) make decisions that less benefit Alice’s values.
If correlated agents (with different values) take the analogous decision, then they will make decisions that less benefit Alice’s values.
If Alice decides to gather information, then that provides evidence that some other agents will observe that people-like-Alice choose to gather evidence in situations like this, and that causes them to do something that is worse for Alice’s values.
The only plausible story I know for (1) is similar to the story for why son-of-EDT cooperates using its parent's correlations. Basically: Updating on new evidence might change who Alice’s successor is correlated with. If Alice’s successor becomes correlated with new agents, then her successor might be incentivized to act to benefit those other agents. (Even though initially, Alice has no incentives to benefit those agents.)
I think (2) is only plausible and compelling if Alice updating on information predictably harms agents that Alice is correlated with.
Why is this? Well, let’s say that Alice thinks that it would be better for Bob to take action y’ that’s analogous to Alice choosing to not gather information (decision y), then to take action x’ that’s analogous to Alice’s choosing to gather information (decision x). If this fact convinces Alice to pick y, then I think that Alice should only treat her decision to pick y as evidence that Bob will pick y’ insofar as Bob has some analogous reason to pick y’ — i.e., if Bob wants to acausally influence someone to make decisions that are better for Bob. Either this is Alice, or it’s some other agent that’s trying to acausally influence someone else. Ultimately, I think this loop needs to get back to Alice’s decision about gathering information, or Alice will be in a situation that’s too different from the other agents’ situation, and she won’t be able to exert any intentional acausal influence on them.
I know three plausible stories for how Alice updating on information could predictably harm other agent’s values:
Firstly, the converse of the issue with (1): Updating on evidence can make Alice’s successor seize to be correlated with agents who Alice is correlated with. If so, her successor might choose to not take some opportunities to benefit those distant agents, that the successor would have taken if she had learned less, and the correlations had been preserved.
Secondly, Alice could learn too much about her bargaining position.
If Alice and Bob start out believing that they have a 50% chance of acquiring power in the future — they might be able to benefit from a deal where they try to benefit the other if only one of them is empowered.
But this is only possible up until the point where they learn who is empowered. If Alice learns too much about this before she can make a commitment — that might ruin her incentive to participate in the deal, which could harm Bob.
I think this is a fairly broad class of cases, where learning too much information removes the incentives to take some deals that would have been positive behind a veil of ignorance.
I discuss this more in A market analogy.
Thirdly, if Alice learning new information would let her accomplish more things in the world, and if Alice’s values are partially opposed to some other agents’ values.
In cases where none of the other issues I talk about in this appendix are a problem, I wouldn’t worry about this one. If Alice’s successor is incentivized to care about the same values, and to prefer the same deals, as Alice herself, then it should be good for Alice to empower Alice’s successor. Alice’s successor will, in this case, not harm other values more than Alice herself would have approved of.
But insofar as some of the other issues I talk about in this appendix apply — then giving Alice’s successor more information could hypothetically exacerbate them.
For example, if Alice’s successor learns enough information that she wants to get out of a deal that Alice tried to commit to — it might be bad for Alice’s successor to learn information about how she can get out of the deal.
All of this makes me think that, given the “No prediction” assumption, updating on evidence is not bad for an updateful EDT agent if:
The agent’s correlations with other agents don’t change.
The agent doesn’t learn too much about its own bargaining position.
What sort of an agent would EDT want to hand-off to, in order to avoid these problems?
To solve the first problem, I think they’d want an agent that somehow decides who to (not) benefit based on who the parent-agent was originally correlated with. Based on appendix X, and assuming the “No prediction” assumption, I think they could update on any information that isn’t causally downstream of the parent-agent’s action when inferring who the parent-agent was originally correlated with. But I’m not sure what the exact algorithm looks like.
The second problem doesn’t seem like it should be very difficult, to me. But I don’t know any nice algorithm that solves it.
When does updateful EDT seek evidence about correlations?
How do these results apply to updateful, non-self-modifying EDT agents? I think that similar results about who you are and aren’t supposed to gather evidence about applies — with some extra complications.
In particular, I think updateful EDT agents are inclined to gather evidence that’s relevant to both their current correlations and their future selves’ correlations with others. (But mostly uninterested in evidence that’s only relevant for one of these.)
To be precise: Let’s say that Alice-1 is an EDT agent who’s next decision is made by Alice-2. Alice-1 has an opportunity to pick up a piece of evidence that will inform future Alices. Alice-1 is only interested in benefiting agents who believe they can influence Alice-1. Alice-2 is only interested in benefiting agents who believe they can influence Alice-2.
Here’s a central example of a case where Alice-1 has reason to gather evidence about correlations:
Alice-1 is uncertain about whether she is in the world where Carol perceives herself to have influence over Alice-1, or not. Button c will give information about this.
I.e., d(A-1|C,c=T) is high, and d(A-1|C,c=F) is low.
In addition, that same button gives evidence about whether Carol believes she can influence Alice-2.
I.e., d(A-2|C,c=T) is high, and d(A-2|C,c=F) is low.
In this case, Alice-1 would like Alice-2 to care more about Carol if c=T. Since Alice-2 has her own reason to do so, Alice-1 thinks it’s good to press the button.
But if the button only applied to one of Alice-1 and Alice-2, similar reasoning would not apply:
If the button gave evidence about d(A-1|C,c=T) but not d(A-2|C,c=T), then Alice-2 would not be motivated to act on the information — A-1 would have no reason to gather it.
If the button gave evidence about d(A-2|C,c=T) but not d(A-1|C,c=T), then Alice-1 would not be motivated to inform Alice-2, since Alice-1 doesn’t care about Alice-2’s correlations insofar as they diverge from Alice-1’s. (As argued in 1. Son-of-EDT does not cooperate based on its own correlations.)
Alice-1 will also be interested in gathering information if the button informs Alice-1 and Alice-2 about their respective correlations with different agents that have the same values.
E.g. if d(A-1|C-1,c=T) > d(A-1|C-1,c=F) and…
… d(A-2|C-2,c=T) > d(A-2|C-2,c=F) and…
A-1 and A-2 share values, and C-1 and C-2 share values,
then I think it will often be good for Alice-1 to press button c.
A market analogy
Let’s say you have a large group of people in a room. They all entered the room with some goods, and now they are walking around making trades with each other. In order to allow for smooth multi-person deals, let’s say that they have a common unit of currency. They entered the room with $0, they can borrow any amount of $ at 0 percent interest, and they have to pay back all of their debts before leaving the room.
If this market is working well, Alice’s goods will be consumed by whoever has the highest willingness-to-pay for them (which could be Alice herself). Each person’s willingness-to-pay is determined by two components:
“Relative preference”: How much they value Alice’s goods relative to other goods (including the ones they themself came in with).
“Bargaining power”: The market value of the goods they initially came in with. If they have nothing to offer, then they won’t be able to buy anything.
As a quirk on this: note that Alice will never sell something to someone unless they sell something to someone who sells something to someone … who sells something to Alice. Since everyone needs to pay back their debts before they leave the room, you can’t have one-way flows of money.
I think this story transfers decently well to cases where the only methods of trade are evidential cooperation. If evidential cooperation is working well, Alice will especially work to benefit the values of people who especially care about what Alice does and who has something to offer to the rest of the acausal community.
There are many ways in which the acausal story differs from a simplistic version of the market story:
Just as in the market-story, there can’t be people who only sell or only buy things. (Nor can’t there be groups of people who only sell or buy things to some other group of people). But in the acausal case, it’s worth flagging:
Other than having loops of people, that condition can also be fulfilled by having infinite lines of people, each of whom benefit the next person in line.
The acausal traders are dealing in subjective expected utility, not realized utility. There are cases where deals would be impossible if everyone knew who they were and what they wanted. But once you account for ignorance, the situation can contain loops or infinite lines, so that trade is possible. See section 2.9 of the MSR paper.)
One reason for why people could “especially care about what Alice does” is if she has an uncontroversial comparative advantage at benefitting their values. But it could also be about beliefs — including beliefs that would be strange outside of the acausal case.
For example, if some (possible) people have priors that suggest that Alice is more likely to exist in the first place, then they will care more about what Alice does, and Alice will prioritize benefitting their values. (At least if she does exist.)
Since the acausal case is dealing with universe-wide/impartial preferences, there will be tons of “nosy preferences”, public goods, etc. Definitely not a simple case of everyone having orthogonal preferences and just doing the trades that make themself happy.
But I want to assume the market analogy as background, and zoom in on one particular acausal quirk: That structures in who perceives themself to be correlated with who (and at what strength) influences how much people care about what people do. (I.e.: How highly they value their goods, in the metaphor.)
The section EDT recommends benefitting agents who think they can influence you basically argues that if Alice perceives herself as having acausal influence over Bob, that is very similar to Alice caring more about what Bob does. Therefore, Alice perceiving herself as having acausal influence over Bob increases Bob’s bargaining power (i.e. the market value of Bob’s initial goods), and means that Bob will prioritize benefitting Alice’s values relatively more. (Assuming that Alice’s metaphorical goods have any market value.)
Seeking evidence
Market case
Now, let’s introduce ignorance. Although people are buying and selling goods, they’re not quite sure how much they actually value the goods. They don’t really know that much about the goods, so they don’t know how useful they will be.
Let’s also say that people can investigate the value of their goods. Should they?
If you investigate the value of a good (either your own or someone else’s) that has two consequences:
It changes how interested you are in buying that good relative to other goods.
It changes the distribution of bargaining power, as the market value of the good will go up (or down) if you decide that you value it more (or less).
Effect (1) is a pure public good. With better understanding of who values a good most, they can be allocated more efficiently.
But effect (2) is in expectation neutral or bad:
If people have risk-neutral preferences, it’s neutral. It just moves around value.
If people have risk-averse preferences, it’s bad. You might lose bargaining power or you might gain bargaining power.
If people have risk-seeking preferences… it’s probably neutral? If people have access to randomness, they can already create risk if they want.
So if everyone has a shared prior of each object’s market-value, then people won’t be interested in gathering information that just changes people’s bargaining power. Indeed, it might be best if everyone committed to their current belief about how much bargaining power each person has. And only then investigated the value of all objects, and allocated them to the people with the highest willingness to pay based on the prior bargaining power. (Though I have by no means shown that this is optimal — nor am I particularly confident that it would be.)
Acausal case
So since “A’s perceived influence on B” corresponds to “A’s valuation of B’s goods”, this tells us that Alice will want to investigate who has perceived influence over Alice (so that she can prioritize their preferences) but that she won’t be interested in investigating questions that are only relevant for determining people’s bargaining power.
Also, Alice has no need for information about who she most wants to be helped by. It’s ok if only her benefactors have that information. So she has no particular reason to investigate her own acausal influence on others.
Or perhaps they only cooperate if you can predict them, and your cooperation is conditional on them cooperating against you. This has been studied in the program equilibrium literature. See here for some references.
I’m using “A2T” as opposed to “A2” here because “A2T” is a relevantly different agent from the hypothetical agent “A2F” that observed the evidence to be false.
Or possibly: If there is an infinite line of actors, each of whom can acausally influence the next.
Slight complication: If you do something different from the agent to your right (i.e. you pay when they keep their money, or vice versa), then you will be in a somewhat different epistemic position than the agent to your left, which could weaken your perceived correlation with them. (Since they will see that the agent on their right did something different than the agent on your right.) Nevertheless, I think you probably pay regardless of what you see the agent to your right do. A very brief argument: If we assume that “agent to the right paid” and “agent to the right didn’t pay” are similar epistemic positions, then regardless of which situation you find yourself in, you’ll reason “me paying is evidence that the agent to my left pays, so I should pay”. Since that argument is the same either way, this lends some support to the assumption that “agent to the right paid” and “agent to the right didn’t pay” are similar epistemic positions.
The above was an illustration of possibility. Separately, there’s also a question about whether there exists any positive reason to expect asymmetric beliefs about acausal influence to be rare. If you favor a view of EDT without “objective” entanglement — where there are just agents and their credences — it’s not so clear why symmetry should be the norm. These are strange things to hold beliefs about, and I can easily imagine different agents holding different beliefs due to fairly non-reducible reasons, such as leaning on different heuristics and intuitions. But maybe the view that “it’s just your credences” is compatible with some strong constraints on those credences that often enforce symmetry.
One type of power you can have is “You’re likely to exist in the real world.” So this suggests that instead of helping people who Alice thinks are likely to exist in the real world, Alice will help people who think that Alice is likely to exist in the real world.
Stealing phrasing from a comment by Joe Carlsmith: You want to be doing the dance that you want the people you can acausally influence to be doing. and this dance is: benefiting the people who can acausally influence them, in worlds where that acausal influence is real.
With “on reflection” suitably specified so as to not involve Alice learning “too much” in a way that would predictably reduce acausal influence.
For some intermediate values of eps, the expected value might be positive for just one of the agents. If so, I think the assumption that "pressing the button is an analogous action despite their difference in credences" would be wrong.