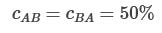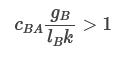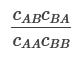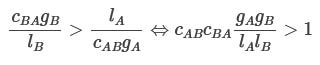Asymmetric ECL
The basic engine behind ECL is: “if I take action A, that increases the probability that a different actor takes analogous action B”. In some circumstances, it’s fairly clear what an “analogous action” is. But sometimes it’s not. This post is about what acausal deals might look like when agents face very asymmetric decisions.
In this post, I will:
Outline a way of thinking about “analogous actions” that might enable ECL deals in highly asymmetric situations. (Link.)
Apply this algorithm in a series of examples, ultimately deriving a formula for when two groups of people will be able to execute a mutually-beneficial ECL deal. (Link.)
Let’s dive into it.
How to think about “analogous actions” in asymmetric situations
(For discussion of many similar ideas, see section 2.8 of Oesterheld (2017).)
In order to reason about asymmetric situations, the main thing that I’m relying on is that the term "action" is broadly defined and meant to include possibilities like "think thought X" or "decide what to do using algorithm Y". For some of those actions, the analogy seems much clearer.
For example, if ECL arguments convinces me to decide to “be more inclined to take actions that help other value-systems (that are endorsed by actors who I’m plausibly correlated with)” or “avoid actions with large externalities on other value systems (that are endorsed by actors who I’m plausibly correlated with)”, then it’s relatively more clear what the analogous decisions are from the perspective of other people. And if all involved parties stick to these resolutions in practice, then all parties can indeed get gains-from-trade. (For an account of ECL that focuses on and recommends “cooperation heuristics” like those I just mentioned, see this post by Lukas Gloor.)
If we go even more abstract, I suspect that ECL would recommend cooperation across even more asymmetric situations. I’ll now give a proposal of such an abstract algorithm, which would ideally also tell us more precisely how inclined we should be to help other value-systems. (The description is pretty cumbersome. I think the rest of the post should be understandable even if you skim past it, so feel free to skip to the series of examples.)
Here’s the idea. I could decide what to do by following the algorithm of trying to approximate the following ideal procedure: Consider all other actors who are trying to decide what to do. Find a joint policy (that recommends actions to all those actors) with properties as follows.1
If this algorithm outputs that policy, and if I follow the recommendations of this algorithm, then I expect my values to be better off than if I naively optimize for my own values.2
This would happen via increasing the probability that other actors follow their part of the policy. So to find a policy with this property, I will estimate how much more likely other actors would be to follow an algorithm similar to this algorithm (rather than naively optimizing for their own values) if I follow this algorithm.3
If this algorithm recommends that policy, then each other actor expects to be better off if they follow the recommendation of the algorithm than if they naively optimize for their own values.
The reason they’d expect this is if they perceived themselves to be increasing the probability that other actors follow their part of the policy. So in order to find a policy with this property, I’ll have to estimate how much acausal influence other actors perceive themselves to have on me and each other.4
The joint policy has various other nice features that make it easy and appealing to coordinate on, e.g:
Pareto-optimality with respect to each participating actor’s beliefs.
Fairly distributes gains-from-trade.
Either it is a natural coordination point or it is robust to other agents’ approximation-algorithms finding somewhat different policies.
(Johannes Treutlein’s paper contains more discussion of the bargaining problem that comes with ECL.)
Compared to naively optimizing for my own values, following the recommendations of a policy output by this algorithm looks like a great deal. It will only recommend that I do things differently insofar as I expect that to positively affect my values (by criteria 1). And this argument is very abstract and general, and doesn’t reference my particular situation. Therefore, it seems plausible that my choice to follow this algorithm is quite analogous to others’ choice to follow this algorithm. In which case the acausal influence in steps 1a and 2a will be high, and so the algorithm can recommend decisions that will give me and others gains-from-trade.5
That said, there are unsurprisingly a number of issues. See this appendix for some discussion, including a concrete example where this algorithm clearly gets the wrong answer.
What would it look like for us to approximate a procedure like the above? In this post, my strategy is to consider a limited number of actors and a simplified list of options, such that the above procedure becomes feasible. The hope is that we can then translate the lessons from such simple cases into the real world.
A series of examples
Prisoner’s dilemma
Let’s say Alice and Bob are playing a game where they can each pay $1 to give the other player $3. Let’s say that, if Alice were to follow the above algorithm (rather than unconditionally refusing to pay), she’d think it was 50 percentage points (50 ppt) more likely that Bob would do the same — and vice versa.
In this case, the algorithm would recommend the joint policy where Alice and Bob both cooperate — since that would make them both expect to get 50%*$3-$1=$0.5. (And it seems like this meets the criteria above: it’s fair, it’s a natural Schelling point, it’s Pareto-optimal, etc.)
Asymmetric dilemma
Let’s say that Alice can pay $1 to give Bob $5, and Bob can transfer any amount of money to Alice. They both have to select their actions before seeing what the other player does. Again, if Alice were to follow the above algorithm, she’d think it was 50 ppt more likely that Bob would do the same (rather than not transferring any money) — and vice versa.
In this case, the algorithm might recommend a joint policy where Alice pays $1 to send Bob $5, and Bob transfers $2.33 to Alice.
This would lead Alice to expect 50%*$2.33-$1~=$0.17.
This would lead Bob to expect 50%*$5–$2.33~=$0.17.
In this case, there’s a wide variety of policies that would leave both parties better-off than if they didn’t cooperate at all. But it seems plausible that the policy that gives both parties equal expected gain ($0.17) would be the most natural one.
Generalizing
Let’s introduce some notation for generalizing the above two cases:
Alice thinks that following the algorithm increases the probability that Bob does the same (rather than doing nothing) by cAB.
(You can read this notation as an abbreviation for “correlational influence that Alice believes she has over Bob”.)
Bob thinks that following the algorithm increases the probability that Alice follows the deal (rather than doing nothing) by cBA.
The algorithm recommends that Alice chooses an option that loses her lA utility and gains Bob gB utility.
The algorithm recommends that Bob chooses an option that loses him lB utility and gains Alice gA utility.
In the simplest, symmetric Prisoner’s dilemma case, where the algorithm recommends that both Alice and Bob cooperates, the relevant numbers would be:
Now let’s formulate the constraints that the algorithm needs to recommend actions that both Alice and Bob benefit from:
Alice expects that following the algorithm gets her
utility. In order for this to be worthwhile, we need
Correspondingly, for Bob, we need that
In the symmetric prisoner’s dilemma, we can verify that both criteria are fulfilled, since
Now, let’s consider the asymmetric dilemma. Although we could simply plug-in the numbers that I used above (Bob transfers $2.33), I want to formulate a general formula that answers the question:
Does there exist any deal that both parties find mutually beneficial, if one party can choose the quantity of help that they send to the other?
Thus, for this general case, let’s say that Bob can adjust his contribution so as to simultaneously linearly increase or decrease both the cost he pays (proportional to lB) and the amount he benefits Alice (proportional to gA) by any positive factor k.
Then, the question “Does there exist any deal that both parties find mutually beneficial?” corresponds to the question “Does there exist any k such that both
and
?”.
Let’s find a general expression that answers that question.
If there’s some k such that both those expressions are larger than 1, then their product must also be greater than 1. By canceling k, we can conclude
Consider instead the case where no possible value of k makes both expressions larger than 1. If so, we can choose a k that makes both expressions equal, where they’re both equal to 1 or smaller. If so, their product will be equal to 1 or smaller, so by canceling k again, we can conclude
Combining these, we can conclude that there exists a k that makes both equations larger than 1 iff:
(For a slightly more detailed derivation of this, see Asymmetric dilemma — more thorough derivation.)
The argument above would work just the same if Alice would have been able to linearly adjust how much she helps Bob, in addition to or instead of Bob being able to linearly adjust how much he helps Alice. So in any dilemma where Alice or Bob can linearly adjust how much they help the other party, they can find a mutually beneficial deal that they’re both incentivized to follow whenever
Large-worlds asymmetric dilemma
Now let’s say that Alice is a paperclip maximizer, who finds herself in a world where she can produce paperclips for $6 or staples for $1. In other parts of the universe, she knows that Bob the staple maximizer lives in a world where both paperclips and staples cost $6 each to manufacture. Let’s assume that Alice thinks that her following the above algorithm would only increase Bob’s probability of doing so by 10 ppt. (And vice versa for Bob.)
Let’s apply the above formula to this case. Alice can create 6 staples for the cost of 1 paperclip, so let’s set gB=6 and lA=1. Bob can create 1 paperclip for the cost of 1 staple, so let’s set gA=1 and lB=1. Then we have
Due to the low acausal influence, there’s no joint policy that recommends Alice to create staples, or Bob to create paper clips, that both Alice and Bob are incentivized to follow.
However, let’s now add the assumption that there’s a huge number of paperclip maximizers (“clippers”) in Alice’s situation across the universe, and a huge number of staple maximizers (“staplers”) in Bob’s situation. And importantly, the clippers don’t expect to be perfectly correlated with each other, and the staplers don’t expect to be perfectly correlated with each other. In fact, Alice expects that following the above algorithm would increase the probability that the other clippers do so by 20 ppt. (And this belief is shared with the other clippers.) Analogously, the staplers only believe that they have a 20% probability of affecting each others’ actions.
Calculating the expected utility then, Alice’s and Bob’s own universes are quite negligibly important. The vast majority of the cost of following through on the deal is the additional 20% probability that other actors with the same values follow the same algorithm, rather than the failure to produce paperclips/staples in Alice’s/Bob’s own universe.
Let’s rewrite the above formula to take this into account. Let’s use similar notation as above, with modifications:
nA is the number of clippers (i.e. actors who share Alice’s values) and nB is the number of staplers (i.e. actors who share Bob’s values).
cAB now refers to each clippers’ perceived influence over each other stapler (and vice versa for cBA). This includes Alice and Bob as special cases — but Alice and Bob no longer have any special relationship that isn’t captured by their relationship to each of the other staplers and clippers.
cAA is clippers’ (including Alice’s) perceived influence on other clippers, and cBB is staplers’ (including Bob’s) perceived influence on other staplers.
With this notation, if we assume that Alice and Bob are a negligible fraction of clippers and staplers:6
In order for a policy to be good for Alice,
In order for a policy to be good for Bob,
Again, if one of the parties can linearly adjust their contribution so as to proportionally increase or decrease both lB and gA, then a mutually beneficial deal is compatible with individual incentives whenever:
For the example sketched above, we would have: cAB = cBA = 0.1; cAA = cBB = 0.2; gA/lB=1; gB/lA=6. Yielding
so a trade is possible.
That’s the main content of this post! If you want to read a few clarifying remarks about this formula, then see the first section of the appendices, right after this..
I extend this formula to situations where actors can gather evidence about how much they correlate with each other in Asymmetric ECL with evidence. (You’d probably want to read When does EDT seek evidence about correlations? before reading that, though.)
Appendices
Some remarks on the formula
A few clarifying remarks on the formula derived above:
The formula is not sensitive to intertheoretic comparisons of utility, or the units that we denominate gains and losses in. gA is divided by lA, and gB is divided by lB, so any linear transformation of those numbers will leave the expression with the same value.
In order for this calculation to make sense, the other paperclippers and staple maximizers must be in the exact same situation as Alice and Bob with respect to all mentioned variables.7 (E.g. degree to which they believe themselves to be influencing other paperclippers and staple maximizers.) And in order for everyone to be able to carry out these computations, and reasonably expect others to match them, all this must be common knowledge.
I’m optimistic that some substantial variation and uncertainty wouldn’t ruin the opportunities for cooperation — but it sure would complicate the analysis and make it harder to find fair deals.
nA and nB cancels out in the final inequality. This means that the number of actors doesn’t affect whether any deal is mutually beneficial. The reason for this is that a deal could be arbitrarily lop-sided to compensate for the greater numerosity on one side.
Note that this assumes common knowledge about the number of actors on each side. If there are disagreements about how many actors are on each side, that could interfere with (or more rarely, enable) a mutually beneficial deal.
Disagreements about the number of actors could naturally emerge from each actor bayes-updating on their own existence, making them (rationally) believe that they are more common.
There are two interesting ways to write
Both point towards the expression being smaller than 1. Both suggest that we care about the relative acausal influence of various groups rather than the absolute level.
One way to write this is
i.e., the ratio between paperclippers’ influence on staple maximizers and paperclippers’ influence on paperclippers — multiplied by the converse.
Since it’s possible to write the expression this way, we can see that (if we hold the other side’s acausal influence constant) the expression only depends on the ratio of how much acausal influence I have on various groups. If I was to proportionally increase or decrease my influence, that wouldn’t change whether a deal was possible or not.
Also, it seems likely that both cAB/cAA and cBA/cBB will be smaller than 1, since agents could generally be expected to have more decision theoretic influence over agents that are more similar to them.
However, they won’t necessarily be smaller than 1.
For example, if I like EDT, but I think that almost no pre-AGI actors are EDT-agents (but lots of AIs use EDT) perhaps I would think that I have more influence on the average AI than on the average pre-AGI actor.
Though in that case: The other ratio will be proportionally smaller (since the AIs would also doubt their ability to influence all the non-EDT pre-AGI actors). So it seems likely that the product should still be smaller than 1.
Another way to write this is
i.e., the ratio between staple maximizers’ influence on paperclippers and paperclippers’ influence on paperclippers — multiplied by the converse.
Again, since it’s possible to write the expression this way, we can see that (holding everything else constant) the expression only depends on the ratio of how much acausal influence various groups have on me (and people similar to me). If I was to proportionally increase or decrease the degree to which others could influence me (and people similar to me), that wouldn’t change whether a deal was possible or not.
Again, it seems likely that both cBA/cAA and cAB/cBB should be smaller than 1. Regardless of what influence the paperclippers have on the staple maximizers, the staple maximizers ought to have more influence — and vice versa. That said, once again, they won’t necessarily be smaller than 1:
For example, perhaps the paperclippers and staple maximizers disagree a lot about decision theory, such that the clippers systematically assign higher correlations than the staplers. If so, one of the ratios could be larger than 1.
Though just as above: I think that in that case, the other ratio will be proportionally smaller. (If the clippers’ high correlations are in the numerator on one side, they will be on the denominator on the other side.
Together, these make me fairly convinced that
should be smaller than 1 in all reasonable situations. That said, the variables in it ultimately describe different actors’ beliefs, and I haven’t nailed down the criteria that the beliefs would have to conform to to guarantee that the expression is smaller than 1.
Asymmetric dilemma — more thorough derivation
If you weren’t convinced by the derivation in Asymmetric dilemma, consider this one.
Let’s say that:
Alice and Bob both have the option to do nothing, in which case they lose no money and send no money to the other agent.
Alice also has the opportunity to lose some money lA to make Bob gain some money gB.
Bob has the opportunity to lose some money klB to make Alice gain some money kgA. Bob is given fixed values for lB and gA, but can choose any positive value for k.
For a joint policy (“deal”) that both agents perceive to be fair and mutually beneficial, Alice thinks that following the deal increases the probability that Bob does the same (rather than doing nothing) by cAB; and Bob thinks that following the deal increases the probability that Alice follows the deal (rather than doing nothing) by cBA.
(You can read this notation as an abbreviation for “correlational influence that Alice believes she has over Bob” and vice versa.)
If so, a joint policy that recommends that both agents send money, and for Bob to use a particular value k, will be perceived to be mutually beneficial iff:
Alice’s expected gain
Bob’s expected gain
Such a k exists iff
One interpretation of this is: If you define gB/lA as Alice’s leverage at helping Bob, and vice versa, then we have that the product of both agent’s perceived influence over each other and leverage at helping each other must exceed 1.
Issues with the algorithm
Here’s a list of some potential issues with the algorithm described at the top:
It’s nice to argue for this procedure under the assumption of common knowledge about each others’ beliefs and uncertainties. But does everything still work when everyone is making wild guesses about each others’ beliefs, each others’ beliefs about others’ beliefs, etc…?
Is it fine to treat good-faith approximations of this as evidence that other people use much more advanced versions, and vice versa?8 What sort of approximations are ok? What if more sophisticated agents will change the algorithm quite a lot, on reflection?
People don’t only have the options to “naively optimize for their own values” vs. “follow this particular cooperation protocol”. They could also look for other cooperation protocols that might benefit them even more. A better version of the algorithm would have to consider such options. (In this post, I ignore this and assume that people are only choosing between naively maximizing their own utility vs. following this cooperation protocol.)
Here’s a concrete version of that last point. If cooperation between actor i and actor j would harm actor k, then k might prefer for no one to cooperate. This would ruin k’s motivation to cooperate with others, unless maybe if we take into account a richer set of counterfactuals and correlations. Here’s a game to illustrate that:
i can press a button that takes $1 from i and k and gives $3 to j.
j can press a button that takes $1 from j and k and gives $3 to i.
k can press a button that takes $1 from k and gives $1 to i and j.
People can transfer money at a $1-to-$1 ratio to whomever they want.
In this game:
Without cooperation: everyone gets $0.
If i+j presses their buttons: i and j get +$2, k get -$2.
If i+j+k all cooperate with each other:
If everyone presses their buttons, i and j get +$3, k get -$3.
Obviously k needs to be compensated in order to be encouraged to participate in the scheme, but there's no amount of money that i and j can transfer to k such that i and j get ≥$2 and k gets ≥$0.
So for every possible 3-way deal, either i and j would have preferred a situation where they entirely excluded k or k would prefer a situation where no one cooperated.
So what will happen?
If you follow my algorithm above to the letter, you’d expect to get an outcome where i, j, and k all get more than $0.
But i (and j) can compellingly argue "if I follow an algorithm where I cooperate with j but screw over k, j will probably do the same, and that's all I want". Since this is strictly better from i’s (and j’s) perspective than following the algorithm above, I think this outcome is more likely.
(Unless the problem is situated in a richer landscape where it's important to treat people fairly and k getting <$0 is unfair here, or whatever.)
That doesn’t necessarily mean that it’s impossible to get maximum gains-from-trade, though. But it would have to go via k arguing "well i and j will cooperate with each other regardless of what I do. But if I help them, that's evidence that they'll transfer money to me, so at least I'll end up at -$1.5 instead of -$2". (Or something like that.)
But I don’t know how to express that in an abstract algorithm, nor whether it’d actually be reasonable for k to have that belief. In particular, an abstract algorithm would need to bake in a different counterfactual than "if I don't cooperate at all, others probably won't cooperate at all" because k would love for others to not cooperate.
This is related to the discussion of “coalitional stability” in this paper.
The distinction between “the algorithm” and “the policy” is subtle but important, so I have bolded the former and italicized the latter, to emphasize the difference.
With “naively optimize for my own values”, I mean optimizing for my own values without taking into account acausal reasons to cooperate with other values. One potential issue with this algorithm is that this might not be the relevant counterfactual. (I’ll return to this later.)
The more acausal influence I perceive myself as having on other actors, the more ok I am with a policy that recommends me to optimize little for my values but recommends others to optimize more for my values. Or in large worlds, where ECL applies: The more acausal influence I perceive myself as having on actors with different values than me, the more ok I am with policies where people with my values optimize little for my values, and others are recommended to optimize more for my values.
Note that my perceived acausal influence on others can be different from their perceived acausal influence on me, because we can have different information. See Asymmetric correlations are possible for an example of this.
If the acausal influences are all 0, then the joint policy will just recommend that everyone optimizes for their own values.
We could relax this assumption by saying that cAA is Alice’s perceived average influence on all clippers, including herself (and likewise for cBB). Since Alice’s influence on herself is 1, this would mean that cAA = (0.2*(n_A-1) + 1). With such definitions for cAA and cBB, the formulas would be correct also in small worlds.
Or have a substantial probability of being in Alice’s and Bob’s situations, with that uncertainty perhaps explaining why the correlations are less than 1.
And if the answer is no: do other, more humble versions of ECL still work?