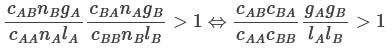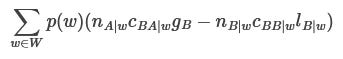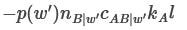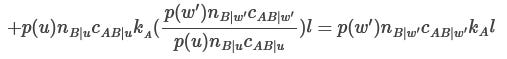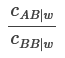Asymmetric ECL with evidence
This post is drawing on two previous posts:
It tackles the intersection of the two: How does asymmetric ECL work in situations where at least one party has the opportunity to gather evidence about how large the correlations are.
More precisely, I investigate a situation where at least one party can:
Linearly adjust how much they help the other party.
Seek out evidence about how large correlations are. (In the sense that I talked about in When does EDT seek evidence about correlations?)
Make commitments about how much they will help the other party given various amounts of evidence.
Just as in Asymmetric ECL, we can ask: Under what conditions will there be a mutually beneficial deal that both parties are incentivized to follow?
The main result is that such a deal exists in similar circumstances as in Asymmetric ECL, except that (for some of the correlations) instead of using the correlations that we believe before taking into account evidence, we can use any correlations such that there is a sufficiently high probability that one of the parties will believe in those correlations after observing evidence.
(When I say “for some of the correlations”: If group B can investigate and gather evidence for correlations, then the above statement applies to cAB and cBB. I.e., actors’ perceived acausal influence on members of group B.)
What do I mean with “sufficiently high probability”? It depends on the risk-aversion of the agents. If one agent can sacrifice arbitrarily much to benefit the other agent arbitrarily much (at a linear rate), and neither party has any relevant bound on their utility functions nor relevant lack of resources, then we can use a similar formula as in Asymmetric ECL but plug-in the best possible correlations that an actor has a non-0 probability of receiving evidence for.
(Again — If group B can investigate and gather evidence for correlations, then the above statement applies to cAB and cBB. I.e., actors’ perceived acausal influence on members of group B.)
When I say “best possible correlations”, I’m referring to the correlations that would most encourage actors to do an ECL deal. (I.e. low correlations with actors who share your values, and high correlations with actors who don’t share your values.)
When I talk about correlations “that an actor has a non-0 probability of receiving evidence for”, I mean correlations such that (e.g.) group B has a non-0 probability of gathering evidence such that group B’s posterior estimate is that the relevant correlations are that large.
In practice, this really tests the assumption of linearity that I was relying on in Asymmetric ECL. Realistic application would have to take into account the realistic bounds on actors’ utility functions and the resources they have access to. (I don’t think that a 10-100 probability of a high correlation significantly changes what deals are possible.)
Nevertheless, in this post, I will just show that the result holds in completely linear situations.
My brief takeaways are that:
Behind the veil of ignorance, agents may be incentivized to commit to very different deals then they would be incentivized to follow later-on. (Because uncertainty enables some deals.)
This results makes me somewhat more optimistic about doing ECL deals with agents that will become very knowledgeable before they need to pay us back.
Quick recap
When does EDT seek evidence about correlations? says:
In some scenarios, son-of-EDT is interested in seeking evidence about what actors would have perceived themselves as having acausal influence over son-of-EDT’s parent agent, and especially benefit those who would have perceived themselves as having a large acausal influence on son-of-EDT’s parent agent.
The main relevance of that post to this post is that I will use a similar notion of “evidence of correlations” as that post uses, and that some of the results are quite similar. (And that other post is better at building intuition for those results.)
Asymmetric ECL says:
Let’s say a group A and a group B have opportunities to benefit each other, where:
nA is the number of agents in group A, and nB is the number of agents in group B, where nA and nB are large.
cAB is the acausal influence (measured in percentage points) that members of group A perceives themselves to have over members of group B. (And vice versa for cBA).
cAA is the acausal influence that members of group A perceives themselves to have over other members of group A. (And similarly for cBB.)
Members of group A have an opportunity to benefit the values of group B by gB at a cost of lA to their own values.
Members of group B have an opportunity to benefit the values of group A by gA at a cost of lB to their own values. Furthermore, they can adjust the size of this benefit and cost linearly, such that for any k, they can choose to benefit the values of group A by kgA at a cost of klB.
Then:
In order for a policy to be good for group A,
In order for a policy to be good for group B,
Which means that, if one of the parties can linearly adjust their contribution so as to proportionally increase or decrease both lB and gA, then a mutually beneficial deal is compatible with individual incentives whenever:
Example to give intuition
Say Alice and Bob are about to decide what to do with their resources.1 Alice can pay $2 to give Bob $4. Bob can pay $2 to give Alice $4 or pay $3 to give Alice $6. Before making a choice, Bob observes whether the correlation between Bob and Alice is 0.8 or 0.2. The higher value obtains with probability p (according to both's prior). Alice makes no such observation. Their shared prior is that the correlation is
Call this cp, the correlation according to the prior.
Imagine that before Bob observes the value of the correlation, they try to arrive at some deal. First consider the following deal:
Regardless of how much correlation there is, Bob and Alice both pay $2 to give the other player $4.
Assume that Bob’s and Alice’s correlations on the decision “doing their part of this deal vs. not sending any money at all” is as I described above — if this assumption would make the deal net-positive for both players.2
The expected gain of accepting this deal (relative to not accepting it) to each of Bob and Alice is:
This is positive (i.e. Alice and Bob are both incentivized to take the deal) if cp>0.5, which is true iff p>0.5.
Now instead imagine that they were deciding whether to make the following deal:
Alice pays $2 to give Bob $4.
Bob commits to paying $3 to give Alice $6 if correlation is high (0.8). Bob doesn't pay anything if correlation is low (0.2).
Imagine again that the decision of whether to accept this deal is correlated as per the above numbers.
Then the expected gain of accepting the deal for Alice is:
This is positive if p > 2/4.8 ~= 40%. note that this lower bound is smaller than the 50% above.
The expected gain for Bob is:
This is positive for all p between 0 and 1. (At p=0 the gain is 0.8. At p=1 the gain is 0.2.)
So, in particular, for values of p between 40% and 50%, the first deal is bad for both players but the second deal is good for both players.
Intuitively, why does this work? The key idea is that the second deal has Bob pay only if correlation is high. Holding fixed the expected (w.r.t. p) amount that Bob gives in a deal, a deal looks better from Alice’s perspective if Bob gives the money in the high correlation case, because those are the possible worlds where Alice’s decision has the most influence on Bob’s decision.
In the above example, note that (unless p is very high) the first deal (where Bob always gives money) gives Alice more money in expectation if both players take the deal ($4 instead or 0.5*6=$3). But Alice’s decision is about whether she herself should take the deal. And if Alice just conditions on her own decision to participate, then the first deal only gets her cp of the $4, in expectation — whereas the second deal gets Alice 0.8>cp of the $3, in expectation.
Let’s generalize
Let’s now study the general version.
We will consider some set of possible worlds W, where for each world w in W:
Both Alice and Bob assign the same prior p(w) to that world.3
Alice thinks her influence on Bob is cAB|w in that word. (And vice versa for Bob.)
Alice and Bob can pay different amounts to benefit each other in different worlds. As a shorthand for the amount that Alice pays to benefit Bob in world w, I will write lA|w. (And correspondingly for Bob.)
We will write the benefit that Bob gains as a monotonically increasing function of how much Alice pays: gB(lA|w). (And vice versa for Alice.)
This means that we can write…
Alice’s expected gain as
Bob’s expected gain as
Similarly to When does EDT seek evidence about correlations?, I will assume that both parties first commit to certain policies (based on what would give both parties high expected utilities) and then they make observations about what world they are in. Also similarly: The parties never get to observe information about each other, including what commitments the other party made. The only relevant information they get is evidence about correlations.
How should Alice and Bob choose lA|w and lB|w to maximize expected benefits to both parties? (As they might want to do if they’re selecting their policy using a similar algorithm as the one described here.)
In the above formula:
lA|w is multiplied by p(w).
gB(lA|w) is multiplied by cBA|w and p(w).
So Alice should choose especially high lA|w in worlds where Bob’s acausal influence on Alice cBA|w is especially high. (Echoing the conclusions from When does EDT seek evidence about correlations?)
Let’s extend this to a dilemma with large groups in large worlds. As previously outlined in the section large-worlds asymmetric dilemma (in the post Asymmetric ECL), group A would normally receive an expected utility of:
Extending this to our new setting:
Group A’s expected gain is
Group B’s expected gain is
How should group A and group B choose lA|w and lB|w, here?
lA|w is multiplied by nA|wcAA|w.
gB(lA|w) is multiplied by nA|wcBA|w.
So group A should choose higher lA|w in worlds with a higher value of cBA|w and a lower value of cAA|w, i.e., in worlds where members of group B have surprisingly much acausal influence on them, and members of group A have surprisingly little acausal influence on each other.
Note that nA|w feature in both expressions, so updates on that number doesn’t clearly affect whose values should be benefitted.
Assuming linearity
Let’s be more precise about the options of group A and B:
Let’s say that members of group A get no information about what world they are in. So they need to choose a single value of lA|w for all w. Furthermore, let’s say they can either choose to make this 0, for which case gB(0)=0, or a specific other number lA. To represent gB(lA), let’s simply write gB.
Let’s say that members of group B get complete information about what world they are in, so they can freely distinct values for all lB|w. Furthermore, let’s say that they can freely choose any non-negative value for lB|w, and that gA(lB|w) is directly proportional to lB|w. Since it’s directly proportional, let’s write gA(lB|w)=kAlB|w.
This means that:
Group A’s expected gain is
Group B’s expected gain is
Here’s something surprising, that we can now conclude: In order to maximize the expected value that both actors get, group B should only benefit group A (i.e., chose non-0 lB|w) in the world(s) where the ratio
is the highest. Why?
Let’s say that there is some world u that maximizes
Let’s say that lB|w’=l>0 for some other world w’ where
(i.e., group B helps group A in some world where the ratio isn’t the highest.)
Then, if the joint policy (recommended by the algorithm) instead recommended group B to:
Decrease lB|w’ by l (i.e. set lB|w’ to 0).
Increase lB|u by
How much would group A’s expected utility change?
Due to getting less utility in world w’:
Due to getting more utility in world u:
Since these are equal, group A’s expected utility would be unchanged.
How much would group B’s expected utility change?
Due to losing less utility in world w’:
Due to losing more utility in world u:
Summing these together, we can factor out some numbers and get:
By assumption,
So this will increase group B’s expected utility.
This shows that for every policy that recommends group B to benefit group A in world that doesn’t maximize
there’s a different policy that is Pareto-better. So if the algorithm only recommends Pareto-optimal policies, it will only recommend policies where group B only benefits group A in the world(s) with maximum
Note that this crucially relies on the assumption that group A’s gain is directly proportional to group B’s loss, and that group B can increase their loss arbitrarily much.
When is a deal possible?
Now, as I did in Asymmetric ECL, let’s try to find out when it is possible for group A and group B to find a mutually beneficial deal.
Based on the above argument, we know that group B will only benefit group A in the world where
is the highest. Let’s call this world u. We can then write:
Group A’s expected gain is:
Group A’s expected gains are larger than 0 if and only if:
Group B’s expected gain is:
Group B’s expected gains are larger than 0 if and only if:
By a similar argument as made in section “Generalizing" of Asymmetric ECL, it is possible for group B to pick a value of lB|u that makes both these expressions larger than 1 whenever the product of them is larger than 1. I.e. when:
This is similar to the main result in Asymmetric ECL. That result said that a deal was possible whenever:
The only differences are that:
We’re writing kA instead of gA/lB. This is just a difference in notation — they represent the same value.
Instead of cAB/cBB we have cAB|u/cBB|u — i.e., we only care about what that ratio is in the world where it’s maximally large.
Instead of cBA/cAA we have
— i.e., we care about the average correlations weighted by the probability of worlds and population size. If population size is independent from cBA|w and cAA|w, then this is simply equal to the expected value of cBA|w divided by the expected value of cBB|w.
What conclusions can we draw from this?
As I mentioned at the start: The assumption of unbounded, linear utility function and ability to pay isn’t realistic. For example, if we apply this lesson to ECL with AI, I don’t think that a world u such that p(u) = 10-100 and cAB|u/cBB|u=1 should make us act just as if cAB/cBB=1.
In particular, some ways in which the unbounded, linear assumption can fail:
Ultimately, I think that utility functions should be bounded, even if they’re linear in some regime. For sufficiently small probabilities, and sufficiently large values of lB|u, we might get pushed outside of that regime. At some point, concerns about Pascal's mugging seem to bite.
A natural way in which linearity can fail is if the AI runs out of resources to pay us with. That seems significantly more likely for small probability of large values of lB|u.
Maybe you just never thought that a linear utility function was a reasonable match to your own values. (In which case the small probability of large utility, introduced here, would increase the degree to which that assumption yields bad conclusions, from your perspective.)
Nevertheless, I think this does push towards somewhat greater optimism about ECL deals with agents that can become knowledgeable and benefit us afterwards. If the probability of a high cAB|w/cBB|w isn’t too low, but is on the order of 10% or so, then maybe the argument in this post is just fine, and we should be happy with a 10% probability of getting a 10x larger benefit in those worlds.
Another take-away is: Behind the veil of ignorance, uncertainty about correlations may incentivize agents to commit to very different deals than they would be incentivized to follow later-on. All of this math relies on certain actors making ECL deals when they are ignorant about who they are correlated with — which could enable deals that would otherwise not be feasible. This is very sensitive to the initial probability distributions that agents start out with. Accordingly, this raises questions about when agents will (and should) first start making commitments. And about whether there’s any more principled way of handling this stuff then to be updateful until the day that you start making commitments, and subsequently letting that time-slice’s beliefs and preferences forever change how you act.
Thanks to Caspar Oesterheld for this example.
If this assumption would only make the deal net-positive for one player, then that’s an important asymmetry that would make the correlations implausible. This first deal can’t be asymmetric in this way — but we’ll soon look at a more asymmetric one.